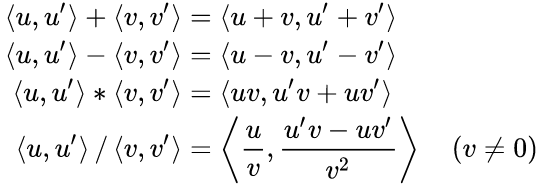Hindsight (noun) – understanding of a situation or event only after it has happened or developed. Ex.: With hindsight, I should never have gone.
The biggest revelations people have are, typically, tied to realization of something that is obvious in hindsight. This revelations can be funny and joyful, sometimes in the most awkward way. They also can be heart-braking and devastating. But one way or another – they are very deep on emotional and rational levels.
You won't have a hard time to think of such revelations in humankind history. Archimedes' principle, shape of Earth, auto differentiation… wait, what? Auto… how, again? Like, switching from Hyundai to Lexus to differentiate from your losers-schoolmates?
Year 2012 marked the most important milestone in Machine Learning, so far – Alex Krizhevsky won an annual competition on image recognition by a large margin. As much as we're happy for Alex, obviously, the fact of his winning and the large margin is not the milestone itself. This year was the year when a critical mass of Machine Learning community realized a plain obvious (in hindsight) set of ideas:
-
Evaluating function derivatives with auto differentiation is MUCH better from a practical standpoint than using numerical or symbolic differentiation.
-
To solve an ill-defined problem you need a lot of sample data to make it better-defined.
-
It's more practical to perform a set of simple embarrassingly parallel operations on a device designed specifically for that (i.e. GPU)
Each of the 2 latter items deserves an article of its own, so I'll mainly focus on the first item.
When I was studying computational methods in the university, they were only teaching 2 approaches to differentiation – numerical and symbolic:
-
numerical is when you evaluate the function in 2 "close" points and divide by the distance between them, and
-
symbolic is when you store the equation for your function and you apply differentiation rules to get the explicit equation for the derivative.
Essentially, this would be the first 2 options that come to mind if you ask a mathematician to think about the problem for 5 minutes. Obviously, both of these approaches have deeper developments, like, Runge-Kutta methods, that overcome certain shortcomings in practical applications. But they don't change them on fundamental level.
Now here's a treat for you, algebra lovers. Imagine an abstract number with the
property $ \varepsilon^2 = 0 $ (similar, to a more widely known $ i^2 = -1
$). We can build a number, like, $ u + u'\varepsilon = (u, u') $ and see how
the arithmetic with such numbers looks like (the images are taken from the
Wikipedia article):
Looks familiar? The second ("imaginary") term, actually, abides to the rules of differentiation! In other words, if instead of operating with real numbers we switch to operating with these dual numbers, we can evaluate the derivative of any function simultaneously with the function evaluation.
If your background is more in programming – imagine that you've implemented a class in C++ and overloaded the arithmetic operators to follow the just described rules. You pass the objects of this class to any template function and without any modifications, it gives you not only the value, but the derivative of the function as well. And since it's C++ – it can use loops, ifs and whatnot!
This and similar approaches are called, automatic differentiation. It's a whole new approach that takes best of both worlds – it's as simple as the numerical differentiation (actually, even simpler once you realize it!) and it avoids a lot of its shortcomings, like, division by small values and evaluation of the original function at multiple points – something that was, typically, attributed to symbolic methods (much more complex both to implement and execute).
This is, truly, the case of joyful and happy revelation, obvious in hindsight. It also answers one the questions I've had unanswered for a long time – why in math differentiation is easy and integration is hard, but in programming – it's the other way around? Turned out the answer was – we were doing differentiation the wrong way!
Now, you may still be wondering – what does automatic differentiation has to do with Alex Krizhevsky and Machine Learning breakthrough of 2012? Well, if you think about it – neural networks are really just complex functions built out of simple (i.e. easy to differentiate!) functions using simple arithmetic operations (i.e. EASY TO DIFFERENTIATE!). And back propagation is nothing else than an autodiff method to evaluate the derivative (i.e. gradient) of the loss function. (Let's leave all analogies with how the brain works and the "neural" linguistic around that on the conscience of people who build them.)
In other words, Alex Krizhevsky showed the community a practical way to apply all the tools together:
-
Build a big-enough dataset (best known method to formulate an ill-posed problem, so far).
-
Build a "solving function" out of simple functions and simple operations.
-
Don't be afraid of the size of the dataset and function complexity since you'll be working with them efficiently – using auto differentiation on math side and GPUs on the computational side.
To conclude, here's the link to an article dated 2009 (!) with the title that has "The most criminally underused tool in the potential machine learning toolbox" as a substring. Can you guess what's this guy talking about?